Запис децималног разломка
Децимални број је разломак написан децималним записом, који се састоји од два скупа цифара одвојених зарезима. Цифре лијево од децималне тачке означавају број цијелих бројева које дати разломак садржи. Бројеви на десној страни зареза, названи децималама, означавају број основних децималних разломака (десетине, стотине, хиљаде дијелова) које дати разломак садржи. Разломци који у називнику имају децималне јединице (10, 100, 1000 итд.) Називају се децималним разломцима, а основни децимални разломци су они код којих је бројник 1 (1/10, 1/100, 1/1000 итд.) .
Децимални запис разломка може бити коначан (садржи коначно много децимала) и бесконачан (садржи бесконачно много децимала). Ако је последња (крајње десна) децимала цифра 0, она није записана (сувишна је).
Пример децималног разломка:
а) завршни децимални запис:
![]()
Слика 1 представља број цијелих дијелова, слика 8 број десетинки, слика 7 број стотина, а слика 5 број хиљадитих дијелова; цифре иза зареза (8, 7, 5) су децимални бројеви 1.875;
б) бесконачни децимални запис:
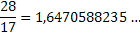
Заокруживање децималних бројева
Бесконачни децимални запис замењује се коначним децималним записом поступком који се назива заокруживање децималних бројева. Пошто је направљена грешка заокруживања, користе се одређена правила како би била што мања:
1) ако је прва цифра коју треба одбацити 0, 1, 2, 3 или 4, тада се последња цифра не мијења, на пример:
• 2,61 ≈ 2,6
• 5.093 ≈ 5.09
• 8.3274 ≈ 8.327
2) ако је прва одбачена цифра 5, а након ње има више цифара, последња цифра се увећава за 1, на пример:
• 3.156… ≈ 3.2
• 7.4759… ≈ 7.48
• 9.2854… ≈ 9.29
3) ако је прва одбачена цифра 5, а после ње више нема цифара, онда је последња цифра:
а) не мијења се ако је парно, на пример:
• 0,85 ≈ 0,8
• 4.345 ≈ 4.34
• 7.6125 ≈ 7.612
б) повећава се за 1 (постаје паран) ако је непарно, на пример:
• 1.275 ≈ 1,28
• 3.835 ≈ 3.84
• 5.4915 ≈ 5.492
4) ако је прва цифра коју треба одбацити 6, 7, 8 или 9, последња цифра се увећава за 1, на пример:
• 0,416 ≈ 0,42
• 6.528 ≈ 6,53
• 8,7489 ≈ 8,749

